來到第7天，繼續介紹PLONK，讓大家可以深入地認識PLONK的基礎。
昨天講了PLONK的特點，而它的特點可以在計算速度及控制SRS大小有明顯幫助。

• PLONK的效能

3. 加強證明者的工作效率: PLONK的設計可以進一步減輕了證明者的計算負擔。由於僅需要五個多項式承諾和兩個開放證明，與其他 ZK-SNARK(例如:Sonic)相比的話，就可以看到證明者的工作量明顯減少，但這裡就不討論其他的，專注地討論PLONK，我會在往後另外寫其他文章介紹ZK_SNARK的其他相關知識和生態。回到PLONK，由於證明者的工作量改進令得 PLONK 成為一種高效計算，更對各種想使用零知識證明的應用程式在效能上有很大幫助。
4. 能壓縮SRS(Structured Reference String)的大小: 這樣可以使到PLONK擁有更小的Structured Reference String，這在生成ZK-SNARK證明中擔當一個很重要的角色。在PLONK中，SRS的程度與電路中所出現的門的數量是相等，因為跟其他 ZK-SNARK 相比，所需用到的儲存量可以大幅地降低。透過壓縮的SRS大小，實現了提高效率及可擴展性。

圖表來源: PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge

在圖表中，大家可以看到其他類型在各項細節上的差別。

• PLONK是怎樣做到提升效率?

圖表來源: PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge

在圖表中，大家可以看到其他類型在各項細節上的差別。

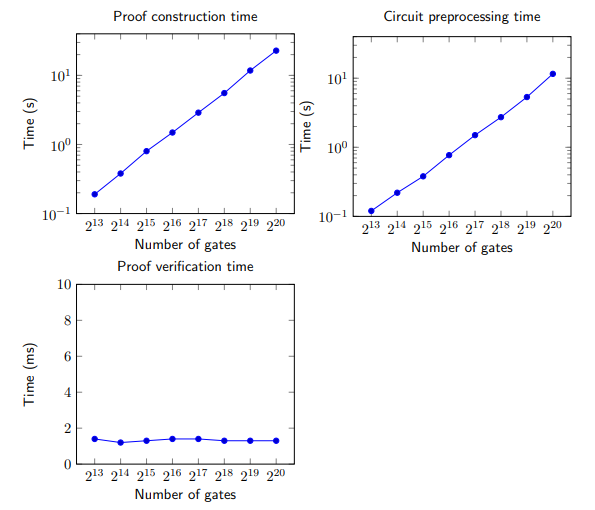
在圖表中的基準測試，可以看到令人信服的結果。廣泛的基準測試展示了 PLONK 的卓越性能，在 23 秒內為一組包含超過一百萬道門的電路創建了證明。而這些數據可以反映出 PLONK 的效率及處理複雜運算的能力。

說到效能，當然要跟Groth16比較一下:

• Groth16
  2016年Groth推出了ZK-SNARK協議，當時協議是基於一組多項式方程式及非對稱配對密碼學所創建。
  基於以"pairing-based"的SNARK所遵循一個簡單的範例，其中證明者使用通用組操作計算一組多個元素，
  而驗證者使用多個配對乘積方程式來進行驗證證明。
  在Groth16方案中，任何具有公共輸入 x 和私密見證 w 的程式的 F(x,w) = y 都可以轉換為算術電路 C。
  為了證明電路C的正確性，必須驗證每道門的正確性。因此Groth16使用二次算術語言 (QAP) 對電路進行編碼轉換。將電路C編碼為QAP的原因是定義多項式

P(z)=Ui(z).Vi(z)-Wi(z)

在對所有乘法門方程式進行編碼時，其中多項式Ui、Vi 和Wi 分別代表左，右，及第 i 道門在 (a1,…,am) 上的事出，它們都是代表電路的線值。
現在我們定義一個目標多項式

T(z)=(z-r1)(z-r2)…(z-rn)

其中 r1、…、rn 是隨機變量，n 表示電路中乘法門的數量。而多項式 P(z)是已定義為可被 T(z) 整除。這意味著存在一個多項式

H(z)，P(z)=H(z)T(z)

所以如果有一個可信任方在隨機點s評估這些多項式（U(z), V(z), W(z)），將它們放入CRS中，然後證明者就做出證明，最後驗證者只需基於收到的證明進行驗證就可以。

• Plonk
  PlonK 協定是可以通過引入通用且可更新的 SRS 解決了一次性的可信設定問題。換言之不同程式可以共享相同的CRS，只要它們的電路大小不超過CRS限制上限就可以。

其實Plonk與Groth16相似，在Plonk中，每個程式都轉換為乘法門和加法門的算術電路。另外，Plonk證明電路的正確性和一致性的方式都是有所不同的。為了證明Plonk電路的正確性，需要證明每道門的約束以及口之間的關係的有效性。除了多項式方程式的驗證之外，更採用置換證明的數學方法來驗證門之間的複製約束的關係。

• 效率比較
  PlonK 提供兩種變體，一種具有 9(n+a) 組合多項式次數，另一種具有 11(n+a)。前者有較大的證明大小，但與後者相比，證明者計算量減少了約 10%。這裡，n代表乘法門，「a」代表電路中的加法門。
  以下是針對Groth16 和 Plonk 的兩個變體的性能和安全性比較: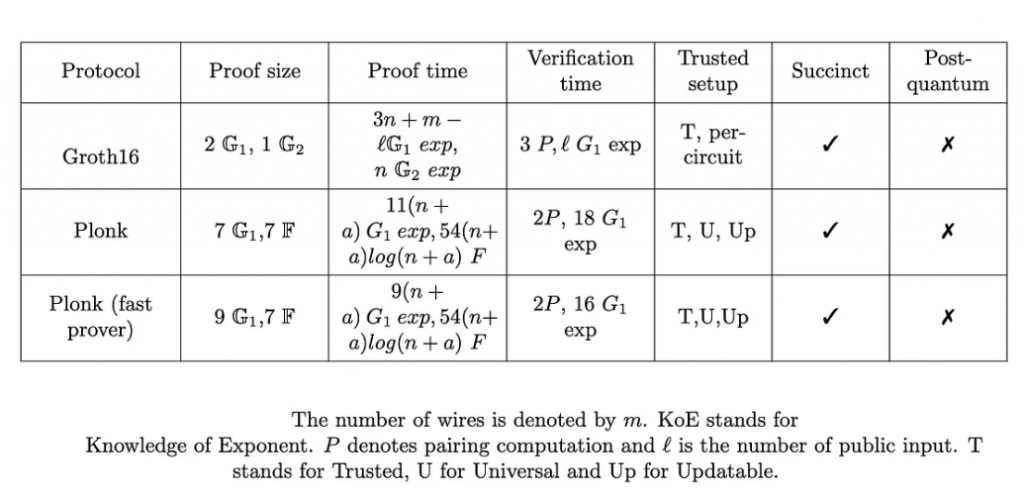
  

• 證明複雜度的分析
  在一般電路中，加法門和乘法門的比例為2：1。在這個比例的電路下，這表示PlonK在證明時間上比 Groth16 會差 2.25 倍。當然，如果是具離線、鏈下情形下可以執行證明產生的能力，就不用擔心證明產生的時間計算。所以集中考慮證明大小，因為它的大小是會影響交易的效率和成本。如果每個群元素都是 F 中的一對 x 和 y 點。

Groth16 證明大小：2G1.(2 F) + 1 G2（計算 4F 元素）= 6F
Plonk 證明大小：9G1+ 7F = 16F

假設每個元素佔用 256 位元。Groth16 證明大小在估計 128 位元安全等級下需要 200 字節，而 PLonk 需要大約 500-1000 字節才能達到同樣的安全水平。

• 小總結:
  由於PLONK具有通用及可更新的可信任設定，所以在這方面是比較優勝。而在Groth16則需要指特的電路的可信任設定，在Plonk中，相同的設定是可以重複用於其他電路。 可更新就是指任何人都可以為可信任設定加上各種隨機性，從而強化對其完整性的信任。另外，PLONK的一個缺點就是它會產出更大的證明大小，要是應用在區塊鏈上就會用上較多Gas fee，如果用於需要經常進行交易的場景時，就會累積花費更多成本。所以Groth16在市場還具有一定的競爭力。

參考:

1. PlonK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge
   https://eprint.iacr.org/2019/953.pdf